TRASLACIÓN DE FIGURAS ~(°w°)~
La traslación pueden entenderse como movimientos directos sin cambios de orientación, es decir, mantienen la forma y el tamaño de las figuras u objetos trasladados, a las cuales deslizan según el vector.En geometría una traslación es una isometría en el espacio euclídeo, caracterizada por un vector, tal que, a cada punto P de un objeto o figura se le hace corresponder otro punto P'.
Dado el carácter de isometría para cualesquiera puntos P y Q se cumple la siguiente identidad entre distancias:
Más aún se cumple que:
*La figura trasladada es idéntica a la figura inicial
Ejemplo:
Para trasladar una figura debemos de considerar lo siguiente :
a) trazar una recta por uno de los vértices de la figura en la dirección deseada.
b) posteriormente se trazan paralelas a la recta dibujada anteriormente, por
cada uno de los vértices de la figura,
c) se elige una distancia d cualquiera para trasladar la figura. Esa misma
distancia se aplica en cada una de las paralelas dibujadas. Uniendo los puntos
obtenidos se obtiene la imagen de la figura dada.

Diapositivas:
http://www.slideshare.net/jdalmagro/traslacin-de-una-figura-plana?v=default&b=&from_search=2
http://www.slideshare.net/plasticabyla/movimientos-en-el-plano-traslacin?v=default&b=&from_search=6
VIDEOS:
La traslación se me complicó un poco en las coordenadas, la verdad no se por que, pero se me hiso mas fácil trasladar las figuras sin las coordenadas, supongo que porque con las coordenadas, tenemos que ser más precisos.
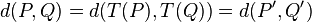
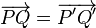
No hay comentarios:
Publicar un comentario