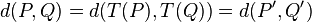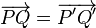ROTACIÓN DE FIGURAS

En geometría y álgebra lineal, una rotación es una transformación al plan o al espacio que describe el movimiento de un sólido rígido alrededor de un eje. Una rotación se diferencia de una traslación, la cual desplaza todos los puntos del sólido por igual y no mantiene puntos fijos, y de una reflexión, que tumban el sólido creando una imagen especular. Las tres transformaciones descritas dejen inalterables las distancias entre parejas de puntos; son isométricas.

Para rotar una figura Se une un vértice de la figura con el centro de rotación mediante un segmento, se traza desde el segmento el ángulo indicado para la rotación y se mide la misma longitud que tiene el segmento anterior marcando el punto imagen.
Se hace lo mismo con cada vértice de la figura y se unen todos los puntos resultantes. 
La figura que se obtiene es la imagen por rotación de la figura original.

El centro de rotación puede estar dentro o fuera de la figura

*La rotación es una transformación que gire una figura sin hacer que cambie su tamaño y forma.

EJEMPLOS >w<










DIAPOSITIVAS:
http://www.slideshare.net/samuelpereiramartinez/clase-1-rotacion-geometrica?v=qf1&b=&from_search=2

http://www.slideshare.net/ignacioaraya95/transformaciones-isomtricas-rotacin?v=qf1&b=&from_search=11


VIDEOS:

         

 Aprendí algunos conceptos sobre rotación, pero aún siento que me falta mucho sobre este tema, sin embargo pude realizarlo en las actividades.
Aprendí a rotar polígonos y aprendí que el centro de rotación puede estar fuera o dentro de la figura, y sigue siendo posible rotarla.

              SUMA DE ECUACIONES CUADRÁTICAS    

Consideremos la ecuación general de segundo grado (ecuación cuadrática) que tiene la forma: .

Resolver esta ecuación implica encontrar el valor o los valores de que cumplen con la expresión, si es que existen.

Analizando la raíz cuadrada, se llega a las siguientes conclusiones:

Si es menor que los resultados de X serán irreales.

Si es mayor que obtendremos dos valores distintos de X reales.

Y si es igual que obtendremos dos valores de X reales e iguales.

Al término se le llama discriminante.

Para resolverlo, necesitamos de ambas formulas:

-4ac
&




Ejemplo:
X² + 2x – 8 = 0      a = 1, b = 2, c = -8
 
 
 
 


 
 
x = -2 ± 6
          2
X =  -2 + 6     x = -2 - 6
           2                  2
 
   x = 4          x = -8
        2                  2
x = 2      x = - 4


ECEPCIONES:
Es posible que no existan soluciones en el conjunto de los números reales. Esto sucede cuando es negativo. En ese caso no es un número real, porque ya se sabe que todo número real elevado al cuadrado, es positivo. (Radicación)
Por ejemplo, en la ecuación , se tiene:

La fórmula en este caso da lo siguiente:

como no es un número real, la ecuación no tiene soluciones reales.

 

 

 Diapositivas:
 

 http://www.slideshare.net/matematicasec29/ecuacion-de-formula-general?v=qf2&b=&from_search=1

http://www.slideshare.net/Compl3xDN/ecuaciones-cuadrticas-por-formula-general?v=qf2&b=&from_search=3

 

 

 *Buena explicación, aún que su voz el muy baja, pero, ahí está :3

Este tema, en lo personal, fue muy fácil, y me enseño que hay que fijarse DEMACIADO en los signos. Aprendí a ordenar los datos : e identificarlos para sustituir mi formula general. También aprendí a sacar el Discriminante y aprendí de memoria ambas formulas.
Aprendí a sacar los valor de X atreves de mi formula general y a saber comprobar mis posibles resultados. 

                       REGLA DE LA SUMA ~|o-o|~

   dos   eventos   A   y   B   son   mutuamente excluyentes,    esta    regla    indica    que    la probabilidad de que ocurra uno u otro de los eventos,   es   igual   a   la   suma   de   sus probabilidades.

 P(A ó B) = P(A U B)

P(A U B) = P(A)+ P (B)

P(A ó B ó...ó Z) = P(A U B U...U Z)

P(A U B U...UZ)= P(A)+ P(B) +... P(Z)

REGLA GENERAL DE LA ADICIÓN

Cuando   los   eventos   no   son   mutuamente excluyentes,  la  probabilidad  de  la  ocurrencia conjunta  de  los  dos  eventos,  se  resta  de  la suma   de   las   probabilidades   de   los   dos eventos.

P(A ó B) = P(A) + P(B) - P(A y B)

 En   la   teoría   de   conjuntos,   la   ocurrencia conjunta hace referencia a la intersección, por lo tanto:

P(A y B) = P(A ∩B)

Entonces: P(A U B) = P(A) + P(B) - P(A ∩ B)

 

Imagina que tienes una balanza en equilibrio:

Si colocamos el mismo peso en los dos platillos, la balanza seguirá en equilibrio:

Esto es lo que ocurre en las ecuaciones al aplicar la regla de la suma, si aumentamos o disminuimos la misma cantidad (" el mismo peso") en los dos miembros de la igualdad ("en los dos platillos de la balanza"), la igualdad sigue siendo cierta para el mismo valor de la incógnita, es decir obtenemos otra ecuación equivalente.
Por ejemplo, dada la ecuación:

x+5=14

Podemos sumar (-5) en los dos miembros obteniendo la ecuación equivalente que nos da la solución:

x+5-5=14-5

x=9

---

En general si tenéis la ecuación:

x+nº1=nº2

aplica la regla de la suma,sumando(-nº1) y obtendrás la solución:

x=nº2-nº1

 Diapositivas:
http://www.slideshare.net/Rockerleo/regla-de-la-suma?v=qf2&b=&from_search=1

http://www.slideshare.net/gevalbe/fundamentos-de-probabilidad-regla-de-la-suma?v=qf2&b=&from_search=3


VIDEOS:

*este no está muy completo, pero tiene la idea.


La regla de la suma fue un tema en el que sin explicación, quizás lo iba a ver algo difícil, sin embargo, al saber la formula y ver la explicación, fue fácil, bueno... aún que  tienes que ser muy paciente para sacar  las probabilidades de los sucesos.

            TRASLACIÓN DE FIGURAS  ~(°w°)~

La traslación pueden entenderse como movimientos directos sin cambios de orientación, es decir, mantienen la forma y el tamaño de las figuras u objetos trasladados, a las cuales deslizan según el vector.

En geometría una traslación es una isometría en el espacio euclídeo, caracterizada por un vector, tal que, a cada punto P de un objeto o figura se le hace corresponder otro punto P'.

Dado el carácter de isometría para cualesquiera puntos P y Q se cumple la siguiente identidad entre distancias:

Más aún se cumple que:

*La figura trasladada es idéntica a la figura inicial

Ejemplo:
Para trasladar una figura debemos de considerar lo siguiente :

 

a) trazar una recta por uno de los vértices de la figura en la dirección deseada.

 

b) posteriormente se trazan paralelas a la recta dibujada anteriormente, por

    cada uno de los vértices de la figura,

 

c) se elige una distancia d cualquiera para trasladar la figura. Esa misma  

   distancia se aplica en  cada una de las paralelas dibujadas. Uniendo los puntos

   obtenidos se obtiene la imagen de la  figura dada.

 

Diapositivas:
http://www.slideshare.net/jdalmagro/traslacin-de-una-figura-plana?v=default&b=&from_search=2

http://www.slideshare.net/plasticabyla/movimientos-en-el-plano-traslacin?v=default&b=&from_search=6

VIDEOS:

* volumen bajo, pero sirve :/

La traslación se me complicó un poco en las coordenadas, la verdad no se por que, pero se me  hiso mas fácil trasladar las figuras sin las coordenadas, supongo que porque con las coordenadas, tenemos que ser más precisos. 
 

                                EJE DE SIMETRÍA (°-°)

Un eje de simetría es una línea de referencia imaginaria que al dividir una forma cualquiera en dos partes, sus puntos opuestos son equidistantes entre sí, es decir, quedan simétricos. En geometría, se usa la expresión "eje de simetría" para los ejes de simetría planos y para los ejes de simetría axial.
La simetría axial, no solo se presenta entre un objeto y su reflexión, pues muchas figuras que mediante una línea pueden partirse en dos secciones que son simétricas con respecto a la línea. Estos tienen uno o más ejes de simetría.
La simetría axial se da cuando los puntos de una figura coinciden con los puntos de otra, al tomar como referencia una línea que se conoce con el nombre de eje de simetría.

Para poder saber cuántos ejes de simetría tiene una figura, debes trazar rectas entre sus distintos puntos, de manera que cada una de ellas, de manera independiente, permita dividir la figura en dos mitades iguales. Si al trazar una recta, esta no divide a la figura en dos mitades iguales, no corresponde a uno de sus ejes de simetría.
Por ejemplo, en este caso, la recta trazada no corresponde a uno de los ejes de simetría, ya al doblar la figura, tomando como indicador la línea que hemos trazado, esta no divide la figura en dos mitades iguales.


Una figura puede tener más de un eje de simetría. Lo que quiere decir es que si tomamos otros dos puntos y trazamos una recta, también podremos obtener dos figuras iguales.

 

 

 Diapositivas:

http://www.slideshare.net/chankimkim/simetra-axial-11512481?v=qf2&b=&from_search=2

http://www.slideshare.net/miriamvega12/simetria-axial-9038204

 

VIDEOS:

 

 

 

Este tema se me hiso demasiado fácil, ya que en algunos otros grados (como en la primaria) ya nos habían enseñado la simetría axial, y los 3 años de estudio en la secundaria hemos tocado el tema de simetrías. Fue fácil, ya que no tiene mucha ciencia y es algo que normalmente, en nuestra vida cotidiana vemos... como el ejemplo más común del "reflejo" o "espejismo", pero igualmente, aprendí que no es necesario "el espejo" para obtener una simetría axial, sino, que también hay formas para sacarle la simetría a los polígonos mediante el uso de la regla o el compás. 

                       SIMETRÍA CENTRAL\ (°O°)/

La simetría respecto de un punto se llama simetría central y los puntos correspondientes, homólogos.
La simetría central, en geometría, es una transformación en la que a cada punto se le asocia otro punto, que debe cumplir las siguientes condiciones:

a) El punto y su imagen estén a igual distancia de un punto llamado centro de simetría.
b) El punto, su imagen y el centro de simetría pertenezcan a una misma recta.

Según estas definiciones, con una simetría central se obtiene la misma figura con una rotación de 180 grados.

Una simetría central, de centro el punto O, es un movimiento del plano con el que a cada punto P del plano le hace corresponder otro punto P', siendo O el punto medio del segmento de extremos P y P

A continuación, se ve un triángulo y su homólogo mediante una simetría central:


Ejemplos:

VIDEOS:

 

La simetría central se me complicó, en el aspecto de que, cuando medía, mis figuras primas, no eran exactamente como las originales, algunas no me salían, mientras que en otras me salín chuecas, o cosas por el estilo, sin embargo, aprendí a elaborarlo correctamente.

                         HOMOTECIA DIRECTA (*u*)/

                               E INDIRECTA \(*w*)

Es la transformación geométrica que no tiene una imagen congruente, ya que a partir de una figura dada se obtienen una o varias figuras en tamaño mayor o menor que la figura dada, para obtenerlas se parte de un punto escogido arbitrariamente, al cual se llama centro de homotecia, del cual se trazan segmentos de recta, tantos como vértices tenga la figura que se va a transformar, se debe considerar otro elemento básico para desarrollar esta transformación, siendo esta una constante, la cual se denomina constante de homotecia que viene a ser la escala en la cual se realiza la reproducción.

Tiene las siguientes propiedades:

• Los ángulos de las figuras por homotecia son iguales ya que tienen la misma medida.
• Los segmentos con paralelos.
• Las dimensiones de dos figuras por homotecia son directamente proporciónales; esta proporción es fijada por la constante de homotecia.

Aquellas figuras que no cumplen con la propiedad de ser paralelos los segmentos se les denomina figuras semejantes, a las que cumplen con todas las propiedades se les denomina figuras homoteticas.

En una homotecia de centro el punto O y razón k:

Si k > 0, A y A′ están al mismo lado de O, y se dice que la homotecia es directa.

Una homotecia es una transformación afín que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor, deja un único punto fijo, llamado centro de la transformación.

 

La homotecia directa es aquella en la que la razón de homotecia es positiva, o dicho de otra forma aquella en la que los puntos iniciales y sus homotéticos quedan en el mismo lado del centro de homotecia.

 

INVERSA:

 

     Si k < 0, A y A′ están a distinto lado de O, y se dice que la homotecia es inversa.       

*Se parte del punto O hacia el lado contrario de la figura original.

 

Diapositivas:

http://www.slideshare.net/lizcasteli/homotecias?v=qf2&b=&from_search=2

 

http://www.slideshare.net/EliteUnlimited/homotecia-10000872?v=qf2&b=&from_search=1

 

VIDEOS:

*Estos primeros 2 videos son de una chica de la misma escuela, de la generación pasada!..muy buena explicación.

 

 

 

En lo personal, fue un tema muy fácil, aprendí que la homotecia directa, nos sirve mayormente para hacer escalas y la figura se puede ampliar o encoger o incluso montar. Mientras que la homotecia inversa se puede distinguir por si constante en "-" (menos), y es muy parecida a la simetría central.